Hi Timber,
vielleicht kann ich den Effekt erklären (allerdings bitte, dabei bedenken, dass ich noch nie einen Helmholtzresonator gebaut habe - alles nur Theorie
):
Ich habe mir die Messungen von Karumba mal im Vergleich zu deinen angesehen. Auf den ersten Blick scheint das Problem ja ähnlich zu sein, insbesondere die Resonanzfrequenzen der behandelten Raummoden liegen ja nah nebeneinander, daher war der Gedanke, eine ähnlich große Kiste zu bauen ja auch erstmal naheliegend.
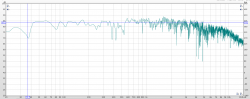
Bei genauerem Hinsehen unterscheiden sich die Situationen aber erheblich: die Messungen von Karumba wurden ja in einem unbehandelten Raum aufgenommen und die Zeitachse reicht hier nicht bis 300 sondern 1000ms! In deinem Raum würde ich die -3dB Bandbreite des Peaks auf etwa 3Hz schätzen. Die Bandbreite des "Karumba"-Peaks liegt dann aber nur bei etwa 0,6Hz (also Faktor 5 kleiner).
Wenn ich Karumbas Helmholtz hier durchrechne, komme ich auf folgende ungefähren Kenndaten:
Bandbreite: 0,8Hz
Q: 45
Koppelfaktor: 0.19
Rt60: 2700ms
Was erst merkwürdig vorkam, war die lange Rt60 Zeit. Aber seit mir klar geworden ist, dass die Raummode selbst über mehrere Sekunden abklingt, kann ich mir wenigstens vorstellen, warum der Resonator hier wirkt: seine Rt60 - Zeit "passt" zum Raum und die hohe Güte besorgt trotz des relativ kleinen Volumens eine gute Kopplung. Hierzu passt auch, dass die Bandbreite von 0,8Hz gut zur Breite der Mode passt.
Deinen Helmholtz konnte ich nicht direkt durchrechnen, da beide Lochsorten (1 und 3cm) einen deutlichen Einfluss auf das Verhalten haben. Daher habe ich ihn einmal mit 30 x 1cm und zusätzlich mit 5 x 3cm Löchern gerechnet (da stellt sich dann ungefähr eine Resonanzfrequenz von 41Hz ein):
5 x 3cm ca.:
Q: 32
Rt60:1740ms
Bandbreite: 1,26Hz
Koppelfaktor: 0,19
30 x 1cm:
Q: 59
Rt60: 3200ms
Bandbreite: 0,69Hz
Koppelfaktor: 0,34
Irgendwo zwischen diesen Werten müsste der HH dann liegen.
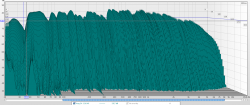
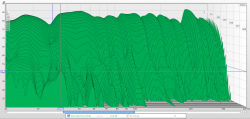
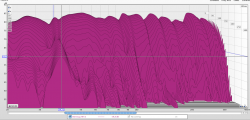
Wenn ich dein Wasserfalldiagramm sehe, sollte die Eigenmode nach vielleicht 600ms um -60dB gesunken sein. Die Bandbreite liegt auf jeden Fall deutlich unter der Bandbreite der Mode. Daraus würde ich den Schluss ziehen, dass der Helmi zu schmalbandig und zu resonant ist, was sowohl die Erhöhung der Zeit als auch die schmalbandige Resonanzspitze erklären würde.
Wenn ich weiter simuliere, komme ich leider auch nicht wirklich auf sehr erfrischende Alternativen. Bei mir ergiben sich (aber bitte auch hier: alles nur theoretisch!) bei 2 Löchern mit je 5,8cm Durchmesser folgende Werte:
Q: 18
Rt60: 942ms
Bandbreite: 2,34Hz
Koppelfaktor: 0,106
mit einem einzigen Loch von 10cm dann:
Q: 9,75
Rt60: 518ms
Bandbreite: 4,26Hz
Koppelfaktor: 0,06
Wird die Resonanzfrequenz durch mehr und kleinere Löcher erreicht, steigen Q, Rt60 und Koppelfktor, während die Bandbreite sinkt. Die Annahme, dass es egal ist, auf welche Art und Weise die Resonanzfrequenz getroffen wird, scheint nach allem was ich weiß nicht zu stimmen.
Die Werte für den Koppelfaktor sind bei den beiden Beispielen nicht mehr wirklich prickelnd und ich würde mal tippen, dass eine wirksame Unterdrückung der Mode dann letztendlich nur mit einem größeren Volumen zu erreichen ist.
Es kann wie gesagt durchaus sein, dass sich alles was ich hier geschrieben habe als haltlos herausstellt, daher bitte genau überlegen, ob du dem folgen willst! Es basiert halt auf den Formeln und Theorien, die ich zum Thema in verschiedenen Quellen gefunden habe und ist in keiner Weise in der Praxis erhärtet.
Vielleicht hilft es ja, um dem Problem näher zu kommen.
Viel Erfolg noch und Gruß, Brausebär