Abtastrate/Samplerate-Mysterium

[Danny-BSF]

Moin Forum.

Da ich hier immer wieder auf User stoße, die eine eigenartige Definition und Zusammenhänge zu dem Thema haben, hier mal ein neues Thema aufgemacht.

Ich selbst habe diesbezüglich nur ein Wissen, bestehend aus Schnibseln aus dem Netz und möchte von euch, die wirklich Ahnung haben, also kein Halbwissen, eine Aufklärung

Hier mal mein Wissensstand und Herleitung:

Abtastrate in (K)Hz, definiert wie oft ein Signal abgetastet wird.
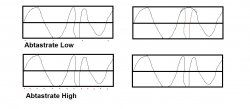
Beispiel wäre ein AD-Wandler, an dem ein analoges Signal anliegt. Der Wandler tastet das Signal ab und schreibt auf der "digitalen Seite" die Signalkurve. Bei einem sich "schnell" verändernden Signal ist die Kurve runder, je höher die Abtastrate ist.

Ein Beispiel:
Angenommen wir sind im Studio und nehmen eine Geige auf, die in sehr hohen Lagen spielt (was anderes fällt mir grad nicht ein). Angenommen, die ganzen Aliens unter uns sind nicht anwesend und wir hören jetzt ein Frequenzspektrum bis 19Khz. Um die Geige möglichst hochauflösend zu digitalisieren wählen wir die Abtastrate 96Khz. Wir nehmen sie auf, wandeln das Signal um in 44,1Khz, weil wir die Geige auf CD haben wollen, vergleichen die Kurven und stellen fest, dass die 44,1Khz Kurve etwas eckiger aussieht (Monsterzoom).

Fragen:
Hören wir einen Unterschied zwischen 96Khz Aufnahme und 44,1Khz CD?
Hören wir einen Unterschied zwischen 96Khz Aufnahme und 44,1Khz Aufnahme?
Je tiefer die Frequenz, desto "langsamer" die Kurve und unrelevanter die Abtastrate, richtig?

So jetzt kommt mein gefährliches Halbwissen:
Meiner Meinung nach ist kein Unterschied hörbar, da das menschliche Gehirn nicht schneller "abtasten" kann, als 44,1Khz.

Ist das alles richtig so?
Stellt sich die Frage, wann es überhaupt Sinn macht eine höhere Abtastrate als 44,1Khz beim Aufnehmen zu wählen.
Habe gehört, dass (einige) Plugins bei höheren Abtastraten "sauberer" arbeiten(Intern?). Hat doch aber nichts mit der, mit 44,1Khz digitalisierten Aufnahme zu tun, oder?

Ich hoffe hier kann Jemand Licht ins Dunkle schaffen,
Dankesehr.

Gruß

Danny

 

[SlimJim]

Ich glaube, du wirfst hier Samplingrate und Bitrate durcheinander...

Mal ganz lapidar gesprochen (technisch gibt's wohl 100000000 Seiten dazu):
Für eine Aufnahme von Frequenzen bis 22KHz benötigstt man 44,1 KHz (also die doppelte Menge, da - auch lapidar gesagt - die Frequenz nach oben und nach unten ausschlägt). Da ein menschliches Gehör allerdings nur bis 20 KHz geht, kannst du jetzt selbst entscheiden, ob du den Unterschied hörst... ich höre ihn definitiv nicht!

Die Bitrate widerrum, gibt an in welchem Zeitintervall die Daten "gespeichert" werden. Diesen Unterschied wirst du definitiv hören! Bei "früheren" digitalen Aufnahmen, wurde oft von "steril" gesprochen - dies war meistens den 8 Bit geschuldet - Als Beispiel: Bei 16 Bit, werden pro Sekunde 640 "Abstufungen" gespeichert - bei 24 Bit 150.000 "Abstufungen"...

Dieser Beitrag ist wissenschaftlich nicht bewiesen - aber so kann ich's mir relativ einfach merken

 

[Danny-BSF]

Hmm, Bitrate mein ich nicht.
Wie gesagt, besitze ich nur Halbwissen, kanns aber vielleicht anhand einer Metapher beschreiben:

Angenommen du guckst ein Film.
Bitrate wäre die Schärfe, oder "Verpixelungsgrad"
Abtastrate der Bildfluss, also Bilder pro Sekunde.

 

[ModulationMatrix]

Eine mit 44,1kHz gesampelte Kurve ist nur eine Näherung der tatsächlichen Wellenform. Jeder Datenpunkt beinhaltet schon einen kleinen Fehler gegenüber dem Original. Wenn du jetzt mit den Daten rumrechnest addieren sich jedesmal kleine Fehler und können dadurch ziemlich groß werden. Wenn du die Rechenschritte hingegen mit einer feineren Auflösung machst und hinterher erst runterrechnest kriegst du ein genaueres Ergebnis. Daher macht es Sinn dass Audiomaterial mit 96kHz gesampelt und verarbeitet wird und erst am Schluss auf 44.1kHz umgerechnet wird.

Für die Bitbreite gilt das gleiche Prinzip.

PS: @SlimJim: deine Zahlenbeispiele für die Anzahl der Stufen sind falsch.

 

[kickback]

Bitrate ist nicht gleich Bittiefe...

Und: wenn man reinzoomt schaut's nur eckig aus, ist es aber nicht.

 

[Danny-BSF]

Danke für die Antworten.

Bitrate ist nicht gleich Bittiefe...

In welchen Zusammenhang denn jetzt Bittiefe?

Und: wenn man reinzoomt schaut's nur eckig aus, ist es aber nicht. cool

Weil alles Sinuswellen sind, oder bei der Umwandlung die Kurven gradegerechnet werden?

Eine mit 44,1kHz gesampelte Kurve ist nur eine Näherung der tatsächlichen Wellenform. Jeder Datenpunkt beinhaltet schon einen kleinen Fehler gegenüber dem Original. Wenn du jetzt mit den Daten rumrechnest addieren sich jedesmal kleine Fehler und können dadurch ziemlich groß werden.

Was sich wie bemerkbar machen kann?

 

[kickback]

In welchen Zusammenhang denn jetzt Bittiefe?

Ich hab damit (8, 16, 24bit) nicht angefangen

Weil alles Sinuswellen sind, oder bei der Umwandlung die Kurven gradegerechnet werden?

Gerade Kurven?

 

[ModulationMatrix]

@Danny: insofern dass es kagge klingt. Stichwort Audio-Aliasing kannste dich auch mal einlesen. Das sind hörbare Artefakte die bei der Verarbeitung mit 44.1kHz entstehen können.

 

[Nordwest7]

Eine mit 44,1kHz gesampelte Kurve ist nur eine Näherung der tatsächlichen Wellenform.

Das ist falsch.
Das Wunder (mathematisch beweisbar) am Sampling ist doch gerade, dass es *völlig* informationstreu ist.
[sub](Lass dich nicht von er schwachsinnige "Wellenformdarstellung" der DAW verarschen, die ist einfach nur falsch, zwischen den Samples ist *nichts*, wie das analoge Signal zwischen den Punkten verlief, bzw. nach Rekonstruktion wieder verlaufen wird, lässt sich auch *nicht* abschätzen, wenn das Signal nicht auf etwa 1/10 der Samplingrate begrenzt ist. )[/sub]

Es gibt eine einzige Bedingung: das Signal muss bandbegrenzt sein, damit eine eindeutige Erfassung bzw. Rekonstruktion möglich ist. Bei Audio ist das immer ein Tiefpassfilter vor dem Wandler, der hat aber mit dem Sampling selber nichts zu tun, er ist einfach notwendige Voraussetzung, damit das System funktioniert.
Außerdem hat es bis heute noch keiner geschafft, einen Tiefpass (um 20kHz), wie er für 44kHz Sampling-Rate nötig ist, zu hören.
Und, um mal einen Maßstab zu setzen: ganz im Gegenteil zu irgendwelchen 5k€ Feld- Wald- und Wiesenmonitoren: der Murks, den die machen, ist problemlos zu hören. Bevor man also lange um Sampling diskutiert, sollte man vielleicht erst mal das Monitoring auf einen nicht völlig schrottigen Stand bringen.


Eine "Näherung" gibt es nur bei der Quantisierung. Da heute (mit 24bit) allerdings nur noch theoretisch, da das analoge Rauschen deutlich größer ist, als der digitale Fehler (der, sobald das Signal groß (Daumenwert 8 bit, bei 24Bit also ca. 96dB unter Vollausteuerung) gegen das LSB wird, zu weißem Rauschen wird).

 

[Danny-BSF]

Habe mal was gepaintet, wie ich mir das vorstelle...

 

[kickback]

Schon mal nicht so schlecht, nur dass, wenn ich deine Grafik richtig verstehe, die höhere Frequenz bei "Abtastrate Low", rechtes Bild, ursprünglich gar nicht durch den low pass filter gekommen wäre.

Wie von Nordwest schon ausgeführt, gibt's einen kleinen Katalog an Bedingungen, unter denen das originale Signal wieder reproduzierbar ist.
Schau dir das Video an.

 

[m_tree]

Man kann Samplerate und Bittiefe als eine Funktion in einem zweidimensionalen Koordinatensystem darstellen. Der Funktionswert, die Bittiefe bzw. y auf der vertikalen Achse ist das Ergebnis der Funktion, die abhängig von der zeitlichen Komponente x, der Samplerate, auf der horizontalen Achse ist.

en.wikiaudio.org

Kein Mensch wird jemals einen Unterschied von 44,1kHz auf höhere Sampleraten hören können. Ein menschliches Baby kann bis 20kHz hören, mit zunehmendem Alter wird diese Grenze immer niedriger (z.B. kann ein 40 jähriger vielleicht noch bis 13 oder 15kHz hören).
44,1kHz ist die Summe der beiden Kanäle, die mit jeweils 22,05kHz abgetastet werden. Die sogenannte Nyquist Frequenz befindet sich bei 20kHz, die restlichen oberen zwei kHz stellen nur die absteigende Flanke des Lowpass Filters dar (Nyquist ist also die Trennfrequenz). Die restlichen 50Hz sind ein Puffer, soweit ich weiß.

Dadurch, dass wir nur maximal bis 20kHz hören können, können wir kleinere Abstände, die durch höhere Sampleraten dargestellt werden können, nicht hören. Harmonische Obertöne von z.B. 15kHz (also 30, 60, 120kHz etc.) können wir nicht mehr hören. Ein Signal mit 96kHz Samplerate kann also höhere Töne als 20kHz darstellen - diese hören wir aber sowieso nicht! Davon abgesehen nehmen die meisten Mikrofone sowieso nur bis 20kHz auf.
Daher: Höhere Samplaraten sehen zwar "detailierter" aus, von den höheren Details (den höheren Frequenzen) haben unsere Ohren aber garnix!

Bei der Bittiefe sieht das allerdings schon anders aus. Die Bittiefe legt im Prinzip den Dynamikbereich fest, der mit einer bestimmten Genauigkeit dargestellt wird. Das Ohr kann extremst kleine Dynamikunterschiede wahrnehmen. Bei einer Rohaufnahme, die sehr dynamisch ist, würde 16bit einen Qualitätsverlust gegenüber 24bit bedeuten.
Die Samplerate legt dann logischerweise das Frequenzspektrum fest. Nichts anderes sind Schallwellen: Frequenz / Tonhöhe (Samplerate) und Amplitude / Lautstärke (Bittiefe).

In 24 statt 16bit aufzunehmen hat allerdings noch einen Grund:
Die Plugins bringen besser und sauberer klingende Ergebnisse in 24bit.

Zum Vergleich:
Mit 16bit können 65.536 Zustände dargestellt werden
Mit 24bit können 16.777.216 Zustände dargestellt werden -> 256 mal mehr als mit 16bit!
24bit hat damit einen um 48dB höheren Dynamikumfang als 16bit.

Dennoch reichen 16bit für fertig gemasterte Aufnahmen aus, weil deren Dynamikumfang verkleinert ist und weil gedithert wird. Dithering ist in dem von kickback verlinkten Video schon ganz gut erklärt. Durch das Quantisieren auf eine geringere Bittiefe entsteht ein zusätzliches Rauschen, das vom Signal abhängig und damit nicht kontrolierbar ist. Der Grund dafür ist, dass durch die größeren Abstände auf der vertikalen (Amplituden) Ebene quasi auf- und abgerundet werden muss. Der Frequenzverlauf wird dadurch verändert, es entstehen andere bzw. zusätzliche Töne - in ihrer Gesamtheit als Quantisierungsrauschen bezeichnet. Dieses würde bei 16bit Rohaufnahmen übrigens bei jeder einzelnen Spur entstehen und sich damit im Mix noch entsprechend summieren.
Dithern glättet das Signal, hat quasi einen Anti Aliasing Effekt. Das quantisierte Signal ist näher am Originalsignal, weniger Quantisierungsrauschen entsteht. Das Dither Rauschen ist formbar und kann so gemacht werden, dass es für uns nicht so laut hörbar ist (z.B., in dem man das Rauschen hauptsächlich auf den Bereich zwischen 15-20kHz legt).
Der Effekt des Ditherings funktioniert so: Liegt das Signal für eine zeitliche Dauer in einem mit der geringeren Bittiefe nicht darstellbaren Bereich, müsste aufgerundet werde. Das Ditherrauschen verändert sich allerdings mehrfach in dieser zeitlichen Dauer und geht über darstellbare Zustände hinaus. Das somit entstehende Durchschnittssignal entspricht dem eigentlich nicht darstellbaren Signal.

Der einzige Grund für Sampleraten jenseits 44,1kHz liegt darin, dass die Plugins bessere Ergebnisse damit bringen. Daher bieten viele Plugins auch Over- bzw. Upsampling an.

Der Grund dafür:
Der Low-Pass Filter an der Nyquist Frequenz, dessen Flanke eigentlich nur von 20 bis 22,05kHz reichen sollte hat auch Einfluss auf das hörbare Signal, weil es keinen perfekten Filter gibt. Mit höherer Samplerate vermindert man diesen Effekt, weil der Lowpass Filter weniger Auswirkung auf den hörbaren Bereich hat.#
Gäbe es einen perfekten Low-Pass Filter, wäre Oversampling nicht nötig.
Evtl. noch besser zu verstehen, wenn man beachtet, dass Oversampling nichts zum Signal hinzufügt, was vorher nicht da war (z.B. mehr "Details").
VOR und NACH dem Mixen und Mastern hat alles über 44,1kHz allerdings schlichtweg keinen Sinn!

Hierzu kann ich übrigens wärmstens das Buch "Mastering Audio" von Bob Katz empfehlen! Dort sind auch noch weitaus mehr grundlegende technische Zusammenhänge sehr gut erklärt.

 

[radio-opa]

Im Prinzip ist dein Halbwissen schon gar nicht mal so falsch. Die Samplingrate bestimmt wie oft ich abtaste und somit auch welchen Frequenzbereich ich darstellen und auch fehlerfrei wieder reproduzieren kann (Stichwort Nyquist Theorem). Die Bitrate gibt an wie fein die Amplitude aufgelöst wird.
Die Sache, dass unser Gehirn nicht höher als 44,1kHz "abtasten" kann ist an sich nicht so ganz richtig dass wir es nicht hören hat mit der menschlichen Hörschwelle zu tun, die um die 15kHz anfängt stark anzusteigen (nähere Infos auf http://de.wikipedia.org/wiki/Maskierungseffekt ). Durch die Mithörschwellen bedingte Maskierungseffekte machen sich auch Codecs wie MP3 zunutze, die auf auditorischen Modellen basieren.

edit: m_tree war wohl schneller und ausführlicher :-/

 

[Soundkraft]

Aus meiner Sicht hat Moduma das schon genau richtig beschrieben.
Je höher Abtastrate und die Bittiefe desto feiner wird das Digitale Raster in das die analogen Quellen gequetscht werden müssen. Das ergibt eine höhere Genauigkeit (weil man die einzelnen Bytes ja genauer plazieren kann). Diese höhere Genauigkeit kommt aber erst so wirklich zum tragen wenn das Material dann weiterverarbeitet wird, denn dann summieren sich die rechnerischen Ungenauigkeiten.

Sagen wir mal du hast nen Eierkarton..so ne Palette mit 8x8 Löchern (Digitales Raster) und dir sagt jemand du sollst das Ei'(Sample) bei Loch 2,3 Horizontal und Loch 4,6 vertikal reinpacken (analoger Wert).
Dann würdest du näherungsweise das Ei bei Loch 2 Horizontal und 5 vertikal reinpacken.
Nun weichst du aber schon 0,3 h. und 0,4 v. Löcher von der Vorgabe ab. Diesen Rechenfehler schleppst du weiter mit dir rum und er wird immer grösser je mehr und je öfter die Position des Eies beeinflusst wird...z.b. durch Effekt-Plugins....aber auch beim reinen Mischen von Spuren müssen die Samplepositionen im Raster verrechnet und ans digitale Raster angenähert werden.

Was sich wie bemerkbar machen kann?

Artefakte.

Kann von "komisch klingen" bis knacksen gehen.

 

[Danny-BSF]

So langsam wirds heller in meinem Köpfchen. Musste mir erstmal zu Gemüte führen, dass das Signal rekonstruiert wird anhand der vorher abgetasteten Samples.
Mit dem Filter verstehe ich jetzt auch.
Es wird, es wird.
Danke an alle

 

[HRF]

Die sogenannte Nyquist Frequenz befindet sich bei 20kHz

Falsch.

Harmonische Obertöne von z.B. 15kHz können wir also nicht mehr hören.

Falsch.

Davon abgesehen nehmen die meisten Mikrofone sowieso nur bis 20kHz auf.

Falsch.

24bit hat damit einen um 48dB höheren Dynamikumfang als 16bit.

Theoretisch, wenn das Rauschen nicht wäre.

Das Dither Rauschen ist formbar und kann so gemacht werden, dass es für uns nicht so laut hörbar ist (z.B., in dem man das Rauschen hauptsächlich auf den Bereich zwischen 15-20kHz legt).

Nur dann wirkt es nicht mehr.

 

[m_tree]

@HRF

Dann ist die Nyquist Frequenz halt bei 20,05. Oder noch woanders? Sags halt, wenn dus besser weißt.

Harmonische Obertöne bzw. Frequenzen sind ganzzahlige Vielfache einer Frequenz. Die erste Oberschwingung von 15kHz wäre also 30kHz.
Bei nicht harmonischen sieht das anders aus. Aber wer lesen kann

Zeig mir doch mal ein Mikrofon, das laut Hersteller über 20kHz irgendwas verwertbares aufnehmen kann. Da gibts nicht viele, wenn überhaupt.

Sagt dir der Begriff Noise Shaping beim Dithern was? Recherchier mal
Übrigens dithert ein höherfrequentes Rauschen (das gleichzeitig durch den psychoakustischen Effekt lauter gemacht werden kann als normales Rauschen) sogar effektiver als niedrigerfrequentes. Siehe meine obige Erklärung zum Dither Effekt.

 

[AndiPaulo]

2 dumme Fragen schräg von der Seite:

Mir ist klar daß man hohe Frequenzen nicht hört.
Aber ist es nicht so, daß bei hoher Sampling-Rate die Höhen (oder was man davon noch hört) genauer dargestellt werden? Theoretisch wird doch ne Sinuswelle von 22 050 Hz bei 44,1 kHz als Sägezahn dargestellt, weil nur 2 x pro Schwingung gemessen wird, bei 88,2 gibt´s doppelt so viele Messwerte.

Nächste Frage:
Ich hab mal gehört daß man eher 88,2 nehmen sollte wenn man auf 44,1 runter will, weil runterrechnen von 96 Rundungsfehler ergibt.

 

[Danny-BSF]

Ein Eckzahn unter 22050Hz bei 44,1khz reicht, um die Waveform zu rekonstruieren.
Daher auch keine Qualitätseinbußen beim Arbeiten mit 44,1Khz... Richtig?

Krieg ich jetzt nen Bienchen, oder muss ich doch nochmal ins Klassenzimmer?

 

[Soundkraft]

Ich hab mal gehört daß man eher 88,2 nehmen sollte wenn man auf 44,1 runter will, weil runterrechnen von 96 Rundungsfehler ergibt.

Dann kann man aber sicher auch gleich bei 44,1 bleiben, wenn man gradzahlig 1:1 ohne dithern runterrechnet. Und wenn man doch dithert würde ich immer das "höherwertige" Ausgangmaterial bevorzugen, dann hab ich ja Ausgangswerte die theoretisch zumindest näher am Quellsignal liegen.