64bit Floating Point Signalfluss

[Nachtschicht]

Hallo,

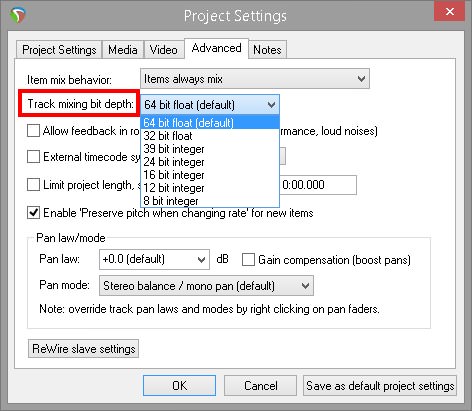
unbestritten wird 64 Bit die Klangqualität zumindest messtechnisch etwas anheben, aber ob das wirklich hörbar ist?
Glaub ich eher nicht.

Mir scheint's, dass mittlerweile die Klangqualität von DAWs seit Jahren, wenn nicht gar seit 10 Jahren oder so, jenseits von gut und böse ist.
Wie will der Hersteller innovativ sein, um die User zum Update oder Upgrade zu überzeugen?
Wo man auch mit einem Cubase 5 noch gut Musik aufnehmen kann...

Alle üblichen notwendigen Plug-Ins gab's damals doch auch schon: EQ, Kompressor, Distortion, Hall/Reverb.

Eine echte Innovation war Meldoyne oder ähnliches, um die Intonation des Gesangs, die Töne gerade zu rücken und auf Tonleiter-Töne zu schieben, wenn der Sänger schief gesungen hatte.
Ich glaube, es gibt mittlerweile auch Tools, um Audio zu quantisieren, wenn also das Timing nicht zum Takt passt. (Kenne ich allerdings nicht, nutze ich also auch nicht.)

Was mich eher interessieren würde, wäre eine Art "objektorientierte" Audio-Part-Verwaltung und -Bearbeitung:
Etwa, im fertig aufgenommenen Song, die Takte 13 bis 20 als "Chorus" zu taggen, um sie als Ganzes mit allen Spuren im Song hin- und her kopieren und schieben zu können.
Wenn man dann in einem der Choruse die Gesangsspur lauter macht, passiert das mit allen so getaggten Chorusen in gleicher Weise - Choruskopie ist Referenz, keine echte Kopie, wie jetzt. Und selbst wenn es keine Referenz-Kopie der Audio-Spuren war, sollten Änderungen in einem der so getaggten Choruse sich auf alle Auswirken.

Weiters, die Automation: Jetzt schreibt man sich z.B. eine Faderautomation für die Gesangsspur. Dann merkt man später im Mix, der Gesang ist insgesamt einen Tick zu leise, die Automation aber in sich durchaus gut. Man will nur die Gesamtlautstärke erhöhen. Was macht man jetzt? Entweder, Faderautomation neu schreiben. Schlecht. Oder aber, als Work-Around, den Gain nach dem Kompressor im Kompressor-Plug-In hoch drehen.
Besser wäre es, direkt am Pegel-Fader, eine Art Global-Pegel einstellen zu können, zusätzlich zum automatisierten Pegel-Fader.


Ich denke, Innovation sollte eher in die Optimierung des Workflows gehen, statt in Pseudo-Klangverbeserungen.

Gruss

nur zur info: gibts eigentlich beides bereits.

das von dir beschriebene szenario mit chorus und so kannst du über die arrangerspur machen. die ist eigentlich ziemlich genau das, was du beschreibst.

global-pegel eines automatisierten faders gibts auch paar varianten. offset-tool in der automation nutzen, offset automation schreiben, gain knopf benutzen (pre-insert) oder halt den letzten insert für einen weiteren gain-parameter benutzen.

 

[LM18]

Hallo,

unbestritten wird 64 Bit die Klangqualität zumindest messtechnisch etwas anheben, aber ob das wirklich hörbar ist?
Glaub ich eher nicht...

Also persönlich, habe ich seit Einführung der 32 BitFloat-Engine (Im Jahre 1904 oder so) mir keine Überlegungen mehr zu einer grundsätzlichen Klangqualität in einer DAW gemacht.

Will sagen, es ist mir tatsächlich komplett gleichgültig was da noch aufgerufen wird - Es macht nur alle verrückt.
Das soll es natürlich auch, das ist wie der Luftsprudler im Aquarium und mischt die Karten etwas neu...

Die größten klanglichen Vorteile finde ich, liegen eher in der Erhöhung der Samplerate.
Da kann man noch was entdecken.
VSTIs, Hall oder Kompressoren klingen anders, vielleicht sogar besser.

Aber Bittiefenfragen stellen sich für mich tatsächlich nicht.
Wenn also jemand da irgendwas positiv klangbeispielhaftes in Händen hält, würde es mich schon interessieren das im Vergleich zu hören.

Aber nur drüber reden...

Ist mir zu mickrig.

 

[Nachtschicht]

Viel Heldengetöse, was ich in den letzten 24 Stunden verpasst habe - aber wenig Ahnung .

Wer von euch kann denn mal den Vergleich vorrechnen, was eine Plugin-Kette aus einem 24-Bit-Sample des Pegels -20dB macht, wenn die drei sequenziellen Arbeitsschritte "-14dB", "+3dB", "+6dB" ausgeführt werden? Einmal für konstante 24Bit-Arithmetik, einmal für 32 Bit Float? Und dann mal die Output-Differenzen am Schluss (wieder auf 24 Bit für die Wandler) vergleichen?

Dafür, dass hier so viel Meinung ist, sollte das eigentlich kein Problem sein.

Und diese simple Bearbeitung ist pipifax gegen übliche DAW-Operationen.

kann man doch in der praxis ausprobieren, ganz ohne informatikstudium
für konstante 24bit arithmetik lässt sich mangels einer verfügbaren daw mit 24bit mixer nichts sagen,
aber 32bit float kann man easy in der praxis ausprobieren (und es ging ja nur um die angeblichen nachteile von 32bit float). zweimal dasselbe signal parallel und sampleallignt abspielen, einen kanal auf unity gain lassen, den anderen durch 3 busse mit jeweils den von beschriebenen pegeländerungen schicken, und dann noch einen vierten bus, der den gain wieder aufholt und die phase dreht.

ergebnis ist ein erfolgreicher nulltest. in manchen daws sind die fader-readouts nicht ganz präzise und du musst statt 5 vielleicht 5,02 aufholen, aber das ist ein separates thema und die engine löscht mit kompensiertem fader-readout wieder komplett aus.

 

[BlueCellarMedia]

aber 32bit float kann man easy in der praxis ausprobieren (und es ging ja nur um die angeblichen nachteile von 32bit float). zweimal dasselbe signal parallel und sampleallignt abspielen, einen kanal auf unity gain lassen, den anderen durch 3 busse mit jeweils den von beschriebenen pegeländerungen schicken, und dann noch einen vierten bus, der den gain wieder aufholt und die phase dreht.

Dir ist schon klar, dass bei identischer Arithmetik dieses Ergebnis herauskommen muss?

Es ging ja um den Unterschied Integer/Float, der hier hanebüchen diskutiert wurde (bis hin zu "16 Bit should be enough for everyone"). Eine Plugin-Kette muss ja nicht synchron in der DAW existieren. Du recordest, gibst Spuren weiter, machst vielleicht Stems, gibst den Mix zum Mastering, dann vielleicht in den DTS-Encoder ... es gibt in dieser Kette genügend Integer-Arithmetik, und die Rundungsdifferenzen sind nun mal bei Iterationen immer größer.

 

[BlueCellarMedia]

Erst du. .

Mach ich sofort, wenn sich von den Diskutanten noch jemand dazu bereiterklärt.

 

[synthpark]

Es ging ja um den Unterschied Integer/Float, der hier hanebüchen diskutiert wurde (bis hin zu "16 Bit should be enough for everyone").

wo wurde denn darüber diskutiert? Wir sind doch nur Musiker. Manche haben Abstraktionsprobleme, andere haben Leseschwäche.

 

[John_Lennon]

Es ging ja um den Unterschied Integer/Float

Nein, eigentlich ging es um den Unterschied Float/Double, was aber im Laufe des Threads leider etwas untergegangen ist.

 

[BlueCellarMedia]

Nein, eigentlich ging es um den Unterschied Float/Double, was aber im Laufe des Threads leider etwas untergegangen ist.

Die ersten 25 Beiträge ging's noch.

 

[BlueCellarMedia]

So, hier mal Tacheles zwischen Integer, Single (32-Bit Float) und Double (64-Bit Float):
Annahme ein Pegel von -20dbVU = -38dBFS
Entspricht maximaler Sample-Amplitude bei 24 Bit von 105606.

Hier die Ergebnisse der simplen Verarbeitungskette:
-14dB:
Integer: 21071 (aufaddierte Abweichung zu 64 Bit Float: 0,167)
Single: 21071,16796875 (aufaddierte Abweichung zu 64 Bit Float: 0,00076)
Double: 21071,1672034603507199790328741

+3dB:
Integer: 29764 (aufaddierte Abweichung zu 64 Bit Float: 0,815)
Single: 29763,81640625 (aufaddierte Abweichung zu 64 Bit Float: 0,0017)
Double: 29763,8147839113917143549770117

+6dB:
Integer: 59387 (aufaddierte Abweichung zu 64 Bit Float: 0,38)
Single: 59386.62109375 (aufaddierte Abweichung zu 64 Bit Float: 0,0049)
Double: 59386.6179880520066944882273674

Fazit:
Rundungsdifferenzen können sich in der Verarbeitung aufheben, aber auch addieren. Sie schwanken nicht vorhersehbar.

Der Präzisionsgewinn bei 32-Bit Float gegenüber Integer-Arithmetik ist deutlich höher, als der Präzisionsgewinn von doppelter Genauigkeit zur einfachen Genauigkeit. Man gewinnt mit 64 Bit Float noch 2-3 Promille Genauigkeit zum Preis der doppelten Hardware-Last.

Bei einer 16-Bit-Verarbeitungskette wären die Differenzen insgesamt dramatischer, da die Integer-Auflösung noch viel geringer ist. Wenn sich Rundungsdifferenzen im unglücklichen Fall addieren, kann der Klirrfaktor durchaus über dem Dithering liegen.

 

[Kosaken-Kaffee]

Also 2 bis 3 Promille kann man schon durchaus hören (und trinken allemal).

 

[ModulationMatrix]

So, hier mal Tacheles zwischen Integer, Single (32-Bit Float) und Double (64-Bit Float):
Annahme ein Pegel von -20dbVU = -38dBFS
Entspricht maximaler Sample-Amplitude bei 24 Bit von 105606.

Hier die Ergebnisse der simplen Verarbeitungskette:
-14dB:
Integer: 21071 (aufaddierte Abweichung zu 64 Bit Float: 0,167)
Single: 21071,16796875 (aufaddierte Abweichung zu 64 Bit Float: 0,00076)
Double: 21071,1672034603507199790328741

+3dB:
Integer: 29764 (aufaddierte Abweichung zu 64 Bit Float: 0,815)
Single: 29763,81640625 (aufaddierte Abweichung zu 64 Bit Float: 0,0017)
Double: 29763,8147839113917143549770117

+6dB:
Integer: 59387 (aufaddierte Abweichung zu 64 Bit Float: 0,38)
Single: 59386.62109375 (aufaddierte Abweichung zu 64 Bit Float: 0,0049)
Double: 59386.6179880520066944882273674

Fazit:
Rundungsdifferenzen können sich in der Verarbeitung aufheben, aber auch addieren. Sie schwanken nicht vorhersehbar.

Der Präzisionsgewinn bei 32-Bit Float gegenüber Integer-Arithmetik ist deutlich höher, als der Präzisionsgewinn von doppelter Genauigkeit zur einfachen Genauigkeit. Man gewinnt mit 64 Bit Float noch 2-3 Promille Genauigkeit zum Preis der doppelten Hardware-Last.

Bei einer 16-Bit-Verarbeitungskette wären die Differenzen insgesamt dramatischer, da die Integer-Auflösung noch viel geringer ist. Wenn sich Rundungsdifferenzen im unglücklichen Fall addieren, kann der Klirrfaktor durchaus über dem Dithering liegen.

WTFFFFF woher hast du denn die Zahlen? Per Hand nachgerechnet? Reschbeggd!

 

[suboptional]

kann man doch in der praxis ausprobieren, ganz ohne informatikstudium
für konstante 24bit arithmetik lässt sich mangels einer verfügbaren daw mit 24bit mixer nichts sagen,

Wenn dir danach ist:

Ich nehm da immer 8 bit integer, dann muss ich mich um die 32 vs. 64 bit float Diskussion nicht kümmern.

 

[synthpark]

Fazit:
Rundungsdifferenzen können sich in der Verarbeitung aufheben, aber auch addieren. Sie schwanken nicht vorhersehbar.

Der Präzisionsgewinn bei 32-Bit Float gegenüber Integer-Arithmetik ist deutlich höher, als der Präzisionsgewinn von doppelter Genauigkeit zur einfachen Genauigkeit. Man gewinnt mit 64 Bit Float noch 2-3 Promille Genauigkeit zum Preis der doppelten Hardware-Last.

Bei einer 16-Bit-Verarbeitungskette wären die Differenzen insgesamt dramatischer, da die Integer-Auflösung noch viel geringer ist. Wenn sich Rundungsdifferenzen im unglücklichen Fall addieren, kann der Klirrfaktor durchaus über dem Dithering liegen.

Aber was heisst das jetzt für die Praxis?
Wie kann ich das bei der nächsten Vocalaufnahme einfließen lassen?
Soll ich die Sängerin mit 64 Bit floaten lassen?

Also bei mir kommt folgendes raus zwischen 32Bit und 64Bit, wenn ich das da einsetze:

20*log10(abs(59386.6179880520066944882273674-59386.62109375)/59386.62109375)

ans =

-145.630587891738

Also eine Abweichnung bei -145 dB gegenüber dem Samplewert.
Was ist jetzt mit Promille? Nix Promille, Prost!

 

[BlueCellarMedia]

WTFFFFF woher hast du denn die Zahlen? Per Hand nachgerechnet? Reschbeggd!

Ja, an den Fingern.

Soll ich die Sängerin mit 64 Bit floaten lassen?

Die Sängerin sollst du flöten lassen. Die digitale Verarbeitung aber floaten. Und dazu bringen dir 32 Bit ausreichend Vorteile. Die anderen 32 kannst du trinken.

 

[LM18]

...Und dazu bringen dir 32 Bit ausreichend Vorteile. Die anderen 32 kannst du trinken.

32 Bit?
Schaffe ich, wenn auch nicht auf Einmal

 

[Loop_Breaker]

...
Die größten klanglichen Vorteile finde ich, liegen eher in der Erhöhung der Samplerate.
Da kann man noch was entdecken.
VSTIs, Hall oder Kompressoren klingen anders, vielleicht sogar besser.

Aber Bittiefenfragen stellen sich für mich tatsächlich nicht.
...

Aber 24bit FLAC Mixdowns klingen einen "Tick besser" als 16bitFLAC Mixdowns, finde nicht nur ich.


BTW: Wenn man in Cubase ein Projekt mit 44,1khz Samplingrate, in den Projekteinstellungen, gemacht hat, und beim Export 192khz angibt, ist Alles, ausser Audio-Spuren (welche aber automatisch konvertiert werden), 192khz?
(mein Multiface kann nämlich nur 96khz, und ich arbeite, um Leistung zu sparen, meist überhaupt nur mit 44,1 khz...)

 

[Burkie]

Aber was heisst das jetzt für die Praxis?

Also eine Abweichnung bei -145 dB gegenüber dem Samplewert.
Was ist jetzt mit Promille? Nix Promille, Prost!

Hallo,
-145dB ist vernachlässigbar, so einfach in der Praxis.

Rundungsfehler sind so ähnlich wie Messfehler, die addieren sich nicht einfach so auf, sondern kompensieren sich teilweise wieder. Da sie unkorreliert sind, addieren sie sich quadratisch: Der effektive Rundungsfehler ist die Wurzel aus der Summer der Quadrate der Rundungsfehler.

Als die Digitale Aufnehmerei, damals noch auf Tonband, losging, wurde mit 16Bit linear quantisiert auf Mehrspurband aufgenommen.
Gemischt wurde, indem das ganze nach analog gewandelt über ein analoges Pult ging, und anschließend mit 16 Bit auf Digital-Tonband aufgenommen wurde.
Summenbearbeitung (Mastern) wurde genauso gemacht, also nach analog gewandelt, bearbeitet, und wieder auf 16 Bit nach Digital gewandelt und aufgenommen.

So haben die Dire Straits ihr berühmtes Brothers-In-Arms-Album aufgenommen, was allgemein als klanglich hervorragend eingeschätzt wurde.

Von daher ist mir in der Praxis diese ganze Bit- und Samplingfrequenz-Huberei egal.

Gruss

 

[Whitenoisestudios]

Also ich möchte jetzt eigentlich lieber nicht in Signaltheorie und Abtasttheoreme sowie Fouriertransformation einsteigen, zumal ich kein Mathematiker bin....

Nur so ein Gedanke...Wenn ich mir einen hochfrequenten Ton oder ein Sinussignal mit beispielsweise 16 KHz ansehe/vorstelle und mit einer Frequenzauflösung/Abtastrate von 48KHz arbeite(48000 Werte pro Sekunde), habe ich auf der X-/Zeitachse ja gerade einmal 3 Datenpunkte zu unterschiedlichen Zeitpunkten um mein "Orignalsignal" in diesem Fall den 16 KHz Sinus möglichst genau zu "rekonstruieren". Da werden dann die 32 Bit/64-Bit float auf der Pegel-/Amplitudenachse ggü. 24 Bit zur originalgetreuen Rekonstruktion des Signals eher weniger ins Gewicht fallen als beispielsweise eine höhere Abstastfrequenz. Eine höhere Samplerate könnte hier eventuell sehr wohl helfen die Rekonstruktionspräzision nachhaltig zu verbessern. Intelligente Filter können hierbei auch noch helfen. Bei 192 KHz beispielsweise, hätte ich schon 12 Datenpunkte mit einer festgelegten Quantisierung(24/32/32 bit float, etc.). Das Signal wäre selbst mit 24 was die Pegel/Amplitudenachse angeht schon sehr exakt aufgelöst/nachgebildet, auf der Zeitachse hingegen immer noch relativ "grob". Was Rundungseffekte und Berechnungen bei langen Signalketten anbelangt, da kann sich das eventuell in der Nachkommastelle bemerkbar machen. Wobei wir ja noch festlegen müssten welchem Standard die float Zahlen folgen, denn die Genauigkeit ist implementierungsabhängig. Die Frage wäre ja auch noch wie das Gehirn und die Ohren das in der Lage sind das überhaupt aufzulösen(vermutlich eher weniger) und wie nachbearbeitende Signalkette/Wandler etc. aussehen...und ob sich das Gehirn eher auf der Zeitachse oder eher auf der Amplitudenachse überlisten lässt....

 

[zille1976]

64 Bit klingt einfach besser.

Wer was anderes behauptet, hat keine Ahnung von Recording und Mixing.

 

[ModulationMatrix]

64 Bit klingt einfach besser.

Wer was anderes behauptet, hat keine Ahnung von Recording und Mixing.

Das war jetzt ein diskussionstechnisches "GOTO 10"