Kleine Abhandlung über Equalizer / Filter

[ModulationMatrix]

Das Startposting ist glockenklar und bringts auf den Punkt. Ein Normalsterblicher kann das verstehen, wenn er will.

Nun, offensichtlich gibt es etliche fragliche Punkte wie man im Thread beobachten kann. Es entspinnt sich eine Diskussion. Ich versteh immer noch nicht warum du das als Majestätsbeleidigung auffasst und so ein Problem damit hast. Ein absolutes Rätsel. Wenn du nicht den "Nachhilfelehrer" spielen möchtest, klink dich doch ne Weile aus, dann diskutieren wir das interessante und anspruchsvolle technische Thema mit Leuten, die emotional kein Problem damit haben. Für genau solche Diskussionen ist das Forum gemacht.

 

[m_tree]

Hast du mich nicht verstanden? Ich hatte darum gebeten, die Finger still zu halten. Wenn du etwas besser weißt, beweise es. Ansonsten sei bitte ruhig.

DANKE!

 

[ModulationMatrix]

Hast du mich nicht verstanden? Ich hatte darum gebeten, die Finger still zu halten. Wenn du etwas besser weißt, beweise es. Ansonsten sei bitte ruhig.

DANKE!

Ruhig, mtree Ich weiß es nicht besser, aber es gibt Unklarheiten. Du möchtest nichts weiter dazu sagen, dann lass es. Kein Problem. Entspann dich Irgendjemand mit technischem Sachverstand wird das schon erklären können. Nochmal: für solche Erörterungen ist das Forum da.

 

[Kuno]

Die Phasenverschiebung ist genau so, wie sie der PluginAnalyser anzeigt.
Also offensichtlich die erste Ableitung *(-1).

Nein, denn der Analyzer zeigt nur die Steigung des Frequenzgangs. Der Frequenzgang ist aber die Folge des Schwingverhaltens und der Phasenverschiebung, nicht die Ursache dafür.
Das ist schlicht und einfach ein Logikfehler.

Ja, du hast hier einen Logikfehler.

Nach deiner Theorie würde ein digitaler Bellfilter also auch vorschwingen. Und das tut er definitiv nicht. Schon garnicht nicht beim Peak.

Eine negative Phasenverschiebung bedeutet nicht automatisch, daß etwas vorschwingen muss.
Ab dem Moment, wo es losgeht, sind die Phasen eben entsprechend verschoben.


Wenn du's nicht glaubst (und auch dem PluginAnalyser nicht traust), kannst du das auch gerne selbst mal nachvollziehen, indem du einfach einen Sinus nimmst, ihn auf z.B. dem linken Kanal durch eine Glocke schickst und auf dem rechten Kanal unbearbeitet lässt.

Dann guckst du dir das Ganze in einem Oszilloskop (Signal Analyzer von rs-met z.B.) an, und schiebst den Sinus per Pitch hoch und runter, so daß du mal durch die Glocke durch fährst.
Du wirst feststellen, daß mittendrin immer ein Punkt ist, an dem die Phase des bearbeiteten Sinus genau gleich der Phase des unbearbeiteten Sinus ist.

 

[Fritz]

Die Phasenverschiebung ist genau so, wie sie der PluginAnalyser anzeigt.
Also offensichtlich die erste Ableitung *(-1).

Nein, denn der Analyzer zeigt nur die Steigung des Frequenzgangs. Der Frequenzgang ist aber die Folge des Schwingverhaltens und der Phasenverschiebung, nicht die Ursache dafür.
Das ist schlicht und einfach ein Logikfehler.

Ja, du hast hier einen Logikfehler.

Nach deiner Theorie würde ein digitaler Bellfilter also auch vorschwingen. Und das tut er definitiv nicht. Schon garnicht nicht beim Peak.

Eine negative Phasenverschiebung bedeutet nicht automatisch, daß etwas vorschwingen muss.
Ab dem Moment, wo es losgeht, sind die Phasen eben entsprechend verschoben.


Wenn du's nicht glaubst (und auch dem PluginAnalyser nicht traust), kannst du das auch gerne selbst mal nachvollziehen, indem du einfach einen Sinus nimmst, ihn auf z.B. dem linken Kanal durch eine Glocke schickst und auf dem rechten Kanal unbearbeitet lässt.

Dann guckst du dir das Ganze in einem Oszilloskop (Signal Analyzer von rs-met z.B.) an, und schiebst den Sinus per Pitch hoch und runter, so daß du mal durch die Glocke durch fährst.
Du wirst feststellen, daß mittendrin immer ein Punkt ist, an dem die Phase des bearbeiteten Sinus genau gleich der Phase des unbearbeiteten Sinus ist.

Wobei man hier leicht eines Übersehen kann:
(Achtung! Hier folgt eine Beschreibung dieser Dinge, so wie ich sie verstanden habe. Wer der Meinung ist, dass da was nicht stimmt, so bitte ich höflichst darum darauf hinzuweisen )

Der Punkt mittendrin, wo die Phasen genau gleich sind, exisitiert ja eigentlich nur in dem Sinn, dass die "Phasendifferenz" der beiden Signale (also zwischen Eingangs- und Ausgangssignal) hier Null ist wenn man eine konstante Gruppenlaufzeit (= linearphasigen Anteil) abzieht;

Tatsächlich wird ja jedes Signal welches einen Filter durchläuft um die Gruppenlaufzeit verzögert.
Nun muss mn sagen, in der Theorie gibt es tatsächlich Filter wo das nicht so ist, die nennt man "akausal" (also quasi "nicht-kausal"). Das ist nebenbei bemerkt mE nach das was die Delaykompensation auch macht (wobei das totale Delay, welches kompensiert werden muss sich auch noch aus anderen Komponenten zusammensetzt denke ich (Blockverarbeitung allgemein, algorithm-delay, etc?!)).

In der Praxis (der Echtzeitverarbeitung) tritt aber die Gruppenlaufzeit in Erscheinung, man könnte auch Latenz dazu sagen, aber darunter verstehen wir hier alle wohl was anderes deswegen ist der Begriff hier wohl zu verwirrungsstiftend und trifft das Ganzewohl sowieso nicht.

Eine DAW ist hier meiner Meinung nach insoweit nicht als Echtzeiverarbeitung anzusehen, als diese einem Plugin das zuvor aufgezeichnete Material schon entsprechend früher zur Verfügung stellen kann.

Jetzt gibt es linearphasige Filter, wo nach Abzug eines linearphasigen Anteils (Delaykompensation; verschieben des Ausgangssignals nach "links" = früher in der Zeit) nur mehr eine Nullphase überbleibt.

Bei allgemeiner Phase liegt der Phasengang dann zentiert um Null und es gibt Anteile, die suggerieren, dass das Ausgangssignal "vorschwingen" müsste- das wäre aber akausal und in realen Systemen so nicht möglich.

Habe schon fertig; später werd ich mir das aber nochmal durchdenken.

 

[Loop_Breaker]

Entschuldigt die vl. dumme Frage: Was hat das ganze mit der Heisenberg-ischen Unschärferelation zu tun? (Deshalb das pre- u. post- ringing? und wenn ja kann vl. Jemand ein bisschen darauf eingehen warum bestimmte Frequenzen "unscharf" werden?)

gLG

 

[LM18]

Loop_Breaker schrieb in #86:

...
Entschuldigt die vl. dumme Frage: Was hat das ganze mit der Heisenberg-ischen Unschärferelation zu tun?

Nichts.
Völlig andere Ebene.

Ein verwackeltes Foto hat auch nichts mit Heisenbergs Theorien zu tun.

 

[Fritz]

Loop_Breaker schrieb in #86:

...
Entschuldigt die vl. dumme Frage: Was hat das ganze mit der Heisenberg-ischen Unschärferelation zu tun?

Nichts.
Völlig andere Ebene.

Ein verwackeltes Foto hat auch nichts mit Heisenbergs Theorien zu tun.

Vielleicht habe ich mich was das betrifft missverständlich ausgedrückt bzw. mit "Unschärferelation" ein missverstnändliches Wort gewählt. Gemeint ist das hier:

https://de.wikipedia.org/wiki/Küpfmüllersche_Unbestimmtheitsrelation

Wie hier steht:

https://de.wikipedia.org/wiki/Energie-Zeit-Unschärferelation

hat das tatsächlich mit dem was man sonst so unter "Unschärferelation" versteht nicht viel zu tun.

Das ist nämlich das hier:

https://de.wikipedia.org/wiki/Heisenbergsche_Unschärferelation

PS: sorry für das viele Theorie-bla-bla-bla, vielleicht interessierts ja wen...

 

[derchris]

Hallo m_tree,

ich habe ein Matlab/Octave/etc. Skript angehaengt, dass den Bode-Plot eines Peak-Filters darstellt, siehe auch das ebenfalls angehaengte Bild. Wie man sieht, entspricht der Phasengang dem vom Plugin-Analyser dargestellten (der ja auch korrekt ist).
Die Gruppenlaufzeit ist in der Tat teilweise negativ (was der Plugin-Analyser bei bedarf uebrigens auch anzeigen kann), das ist aber nichts aussergewoehnliches, siehe z.B. in diesem pdf auf Seite 4.

Das Skript erzeugt ueber die FFT einer Filter-Impulsantwort einen (komplexen) Frequenzgang und zerlegt diesen Amplitude und Phase, die dann dargestellt werden.


gruss, Chris

 

[m_tree]

Wenn du's nicht glaubst (und auch dem PluginAnalyser nicht traust), kannst du das auch gerne selbst mal nachvollziehen, indem du einfach einen Sinus nimmst, ihn auf z.B. dem linken Kanal durch eine Glocke schickst und auf dem rechten Kanal unbearbeitet lässt.

Dann guckst du dir das Ganze in einem Oszilloskop (Signal Analyzer von rs-met z.B.) an, und schiebst den Sinus per Pitch hoch und runter, so daß du mal durch die Glocke durch fährst.
Du wirst feststellen, daß mittendrin immer ein Punkt ist, an dem die Phase des bearbeiteten Sinus genau gleich der Phase des unbearbeiteten Sinus ist.

Ich habe das mal mit verschiedensten Einstellungen getestet. Auf die Idee mitm Oszi bin ich noch garnicht gekommen. Danke

Die Phasengänge entsprechen wirklich der 1. Ableitung des Frequenzgangs. Getestet habe ich nur digitale EQs.

Ich finde das sehr kontrovers, weil man im Zusammenhang mit analogen (bzw. nicht näher spezifizierten) Filtern nur von den Phasengängen aus meinem Eingangspost liest - und die entsprechen ja nun nicht der 1. Ableitung.
Wenn sich die Phasengänge von analogen und digitalen Filtern wirklich so grundlegend unterscheiden, müssten die theoretisch doch auch generell anders klingen, oder?

Ich werde das Startposting jetzt editieren und die Gleichsetzung mit digitalen Filtern rausnehmen.

Den Test mit dem Sinus und dem Oszi werde ich noch mit einem analogen EQ machen, plus REW Messung für den Frequenzgang. Geht aber erst am Donnerstag, weil ich dann erst wieder im Proberaum bin und Zugriff auf analoges Equipment + Interface habe.

@derchris
Danke, das pdf ist sehr interessant.

 

[ModulationMatrix]

Hallo m_tree,

ich habe ein Matlab/Octave/etc. Skript angehaengt, dass den Bode-Plot eines Peak-Filters darstellt, siehe auch das ebenfalls angehaengte Bild. Wie man sieht, entspricht der Phasengang dem vom Plugin-Analyser dargestellten (der ja auch korrekt ist).
Die Gruppenlaufzeit ist in der Tat teilweise negativ (was der Plugin-Analyser bei bedarf uebrigens auch anzeigen kann), das ist aber nichts aussergewoehnliches, siehe z.B. in diesem pdf auf Seite 4.

Das Skript erzeugt ueber die FFT einer Filter-Impulsantwort einen (komplexen) Frequenzgang und zerlegt diesen Amplitude und Phase, die dann dargestellt werden.


gruss, Chris

Danke Chris, sehr lehrreich!


@m_tree: als Lehre aus dem Ganzen; kannst du dir bitte für's nächste mal vornehmen nicht mehr ständig derart aggressiv und beleidigend zu reagieren, wenn mal jemandem etwas nicht klar ist, denn wie man sieht kannst auch du dich irren.

 

[Loop_Breaker]

Loop_Breaker schrieb in #86:

...
Entschuldigt die vl. dumme Frage: Was hat das ganze mit der Heisenberg-ischen Unschärferelation zu tun?

Nichts.
Völlig andere Ebene.

Ein verwackeltes Foto hat auch nichts mit Heisenbergs Theorien zu tun.

Vielleicht habe ich mich was das betrifft missverständlich ausgedrückt bzw. mit "Unschärferelation" ein missverstnändliches Wort gewählt. Gemeint ist das hier:

https://de.wikipedia.org/wiki/Küpfmüllersche_Unbestimmtheitsrelation

Wie hier steht:

https://de.wikipedia.org/wiki/Energie-Zeit-Unschärferelation

hat das tatsächlich mit dem was man sonst so unter "Unschärferelation" versteht nicht viel zu tun.

Das ist nämlich das hier:

https://de.wikipedia.org/wiki/Heisenbergsche_Unschärferelation

PS: sorry für das viele Theorie-bla-bla-bla, vielleicht interessierts ja wen...

Hab was gefunden:
Zitat von
https://books.google.at/books?id=j1...wAg#v=onepage&q=tontechnik heisenberg&f=false
(hoffe der Link funkt) :

Das Problem der endlich Länge des Analysefensters bei der FFT führt auf ein grundlegendes Phänomen der Akustik und Nachrichtentechnik, die Unbestimmtheit von Zeit- und Frequenzverlauf eines Signals. Diese Unbestimmtheit ist eng verwandt mit der Unschärerelation der Quantenmechanik. Je länger ein Analysefenster ist, desto stärker wird das Spektrum zeitlich gemittelt. Bei sehr großer Fensterlänge spricht man auch von LTAS (long time average spectrum, gemitteltes Langzeitspektrum). Dadurch wird die Genauikeit im Frequenzbereich zwar immer großer, aber gleichzeitig im Zeitbereich immer kleiner!
Bei der Einführung der Fourer-Transformation in Abschnitt 4.2.1 taucht diese Problem noch nicht auf. Dort wurde stillschweigend voausgestzt, dass die Signale analytisch beschreibbar und damit jür jeden beliebigen Zeitpunkt vorherbestimmt sind. Anders ist es bei realen Signalen, die zeitveränderlich sind, die also im Zeitverlauf Informationen enthalten. Hier muss man abwägen: Möchte man das Spektrum genau bestimmen? Dann muss man im Zeitbereich mitteln. Und je genauer (schärfer) man das Signal im Frequenzbereich darstellen möchte, desto mehr Information über den zeitlichen Verlauf verliert man, desto ungenauer (unschärfer) wird es im Zeitbereich. Beides kann man nicht haben.
______________________________________________________________

In den 1. Wiki Artikel den Du verlinkt hast steht ausserdem:
https://de.wikipedia.org/wiki/Küpfmüllersche_Unbestimmtheitsrelation


Die küpfmüllersche Unbestimmtheitsrelation oder Unschärferelation der Nachrichtentechnik ist die Aussage der Systemtheorie (Nachrichtentechnik), dass die Zeitdauer oder Einschwingdauer und die Bandbreite eines Signals nicht gleichzeitig beliebig klein werden können.[1] Sie liefert eine auf die Verhältnisse nachrichtentechnischer Systeme angepasste und zur Heisenbergschen Unschärferelation analoge Aussage.


___________________________________________________



Es ist doch Falsch zu sagen wenn man das Signal 180° phasenverschiebt (nicht Phase drehen) und es mit den Original zusammenmischt, dass es sich auslöscht, (außer bei Sinus, Rechteck und so) oder?


gLg

 

[ModulationMatrix]

OK also nochmal zum Thema "Färbungen", oder besser Phasenverschiebung und Nachschwingen (Nachschwingen = Group Delay?). Ich hoffe ich habe es nun basierend auf Chris' Input richtig verstanden, bitte korrigieren falls ich irgendwo einen Fehler habe.

Ich habe es jetzt so verstanden (in Worten da ich keine Graphen zur Hand hab):

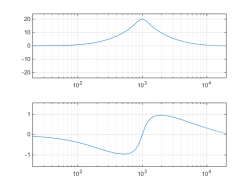
Peak Filter

- Phasenverschiebung punktsymmetrisch zur Peak-Frequenz, jeweils positives und negatives Extrem links und rechts von ihr, null bei der Peak Frequenz selbst.
- Group Delay: achsensymmetrisch zur Peak Frequenz, Extremwert bei Peak Frequenz selbst

Shelving Filter

- Phasenverschiebung achsensymmetrisch zur Übergangsfrequenz, Extremwert bei Übergangsfrequenz selbst
- Group Delay: punktsymmetrisch zur Übergangsfrequenz, jeweils positives und negatives Extrem links und rechts von ihr, null bei der Peak Frequenz selbst


Im Klartext heisst das

- der Peakfilter erzeugt hohes Nachschwingen im Peak, hohe Phasenverschiebungen in den Wendepunkten des FG

- ein Shelvingfilter erzeugt hohes Nachschwingen links und rechts der Übergangsfrequenz (bei den Punkten höchster Krümmung im FG), hohe Phasenverschiebungen bei der Übergangsfrequenz selbst.

------------------------------------------------------

Im Falle des Peakfilters sind also die größten Nachschwinger tatsächlich im Peak zu finden, somit wäre Absenken aus dieser Perspektive neutraler als Anheben.

Beim Shelving Filter ist es egal, auf beiden Seiten der Übergangsfrequenz treten entgegengesetzte Group Delays auf. Anheben oder Absenken macht hier also keinen Unterschied.

------------------------------------------------------

Edit:
Übrigens hier findet man ne Menge schöner Diagramme drin:

http://www.google.de/url?sa=t&rct=j...oICoBg&usg=AFQjCNEfQ4GR--DspPfzCmcjcebpKvlwCQ

Leider fehlten die Diagramme gerade für die Shelving Filter (da war nur der FG angegeben), die hab ich mir daher nach der Definition Group Delay = Ableitung der Phase nach der Frequenz aus Bcccs Plots skizziert.

Interessant fand ich auch die Profile von HP und LP auf Seite 11, obwohl sie die umgedrehte frequency response haben, sind phase response und group delay gleich. D.h. im Fall vom HP wären die "Färbungen" im Durchlassbereich am geringsten.

Ich weiß aber immer noch nicht ob mit Färbungen nicht üblicherweise was anderes gemeint ist, einfach ein verbogener FG oder so. Man sollte sich vielleicht einen besseren Begriff einfallen lassen.

 

[m_tree]

Wie schon gesagt: Bei digitalen EQs scheint die Phasenverschiebung die 1. Ableitung zu sein. Also die Steigung des Frequenzgangs.

Die Gruppenlaufzeit ist wiederrum die Ableitung der Phasenverschiebung. Da wo die Phasenverschiebung sich am stärksten ändert, ist die Gruppenlaufzeit also auch am längsten (bei genauer Betrachtung deckt sich das mit deiner Beschreibung). Allerdings ist die Gruppenlaufzeit auch frequenzabhängig und bei tieferen Frequenzen länger.

Die Gruppenlaufzeit ist aber nicht das Nachschwingen. Das Nachschwingen ist die Folge von der Gruppenlaufzeit.

 

[Fritz]

[...]

Die Gruppenlaufzeit ist wiederrum die Ableitung der Phasenverschiebung. Da wo die Phasenverschiebung sich am stärksten ändert, ist die Gruppenlaufzeit also auch am längsten (bei genauer Betrachtung deckt sich das mit deiner Beschreibung). Allerdings ist die Gruppenlaufzeit auch frequenzabhängig und bei tieferen Frequenzen länger.

[...]

Der Vollständigkeit halber: Die Gruppenlaufzeit kann von der Frequenz abhängig sein.

Bei einem linerphasigen Filter (Phasengang ist eine Gerade) ist die Gruppenlaufzeit (group delay) damit konstant (Ableitung einer affinen Funktion (= Geraden) ergibt einen konstanten Wert). Das bedeutet dass alle Frequenzen um den gleichen Betrag verzögert werden und sich daher auch die Wellenform nicht ändert (abgesehen von der Verzögerung). Das Wellenpaket (die Wellenform) läuft in diesem Fall nicht auseinander ("verschmieren").

Das ist der entscheidende Unterschied eines linearphasigen zu einem Filter mit allgemeinem Phasenverlauf (darunter fallen auch z.B. Minimalphasige Filter).

Siehe die Abb rechts oben in diesem Wiki-Artikel:

https://de.wikipedia.org/wiki/Gruppenlaufzeit

 

[m_tree]

Ich kenne den Wiki Artikel und war genau von dieser Aussage etwas verwirrt. Bin aber jetzt drauf gekommen:

Ein linearer Phasengang ist eine ansteigende Gerade. Wäre die Gerade waagrecht, wäre die Gruppenlaufzeit = Null.

Denn die zeitliche Dauer der Phasenverschiebung ist immer frequenzabhängig und bei tiefen Frequenzen länger als bei hohen. Ist die Laufzeit konstant, muss sich die Phasenverschiebung also konstant ändern.

Werde den Startpost dann entsprechend ändern, wenn ich weiß, wie sich ein analoger Filter verhält.

 

[ModulationMatrix]

Kennt jetzt noch jemand den genauen Zusammenhang zwischen Group Delay und Nachschwingen?

 

[Fritz]

Kennt jetzt noch jemand den genauen Zusammenhang zwischen Group Delay und Nachschwingen?

Sagen wir es mal so: Ich denke nicht, dass die Gruppenlaufzeit die beste Größe ist um Aussagen über das Nachschwingen zu treffen. Da gibt es andere Parameter mit denen das (imo) aussagekräftiger möglich ist.

 

[LM18]

Hier nochmal kurz eine kleine Fundstelle:

http://www.kirchner-elektronik.de/~kirchner/Guete.pdf

Vielleicht mag der Eine oder der Andere daraus noch etwas entnehmen können...
Einfach so.

 

[ModulationMatrix]

Hm, leider sagt er über die Abhängigkeit des Nachschwingens von der Frequenz bzw von der Filter-Kennlinie bei Digitalfiltern nichts genaueres.

@Fritz: kennst du denn da Zusammenhänge?

Also bisher sehe ich keinen Hinweis dass das Nachschwingen im angehobenen Bereich am stärksten ist. Phasenverschiebung und Group Delay haben beide eigene Abhängigkeiten die im Fall von Peak und Shelf sehr unterschiedlich sind. Der Satz "beim Anheben wird die Färbung hervorgehoben" ist so in jedem Fall falsch. Das trifft lediglich für das Group Delay beim Peak Filter zu. Für die Phasenverschiebung haben wir andere Profile ermittelt, und für das Nachschwingen haben wir derzeit noch keine konkretere Abhängigkeit von der Filtercharakteristik, als dass es es größer ist bei hohem Q. Das sollte man auch so differenziert im Startpost einarbeiten, anstatt eine griffige aber falsche Regel anzugeben. Natürlich wird die Färbung durch den EQ mit angehoben, sie ist aber im angehobenen Bereich nicht am stärksten weil sie anderen Abhängigkeiten unterliegt.