Was steckt hinter digitalen Audio-Daten - eine Geheminisentlüftung
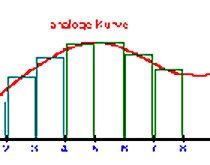
Wer vor 30 Jahren als Musiker eine Mehrspur-Tonbandmaschine besaß, hatte auf einen Schlag ganz viele neue "Freunde" und einen Haufen Schulden. Als dann die Digitaltechnik einsetze, wurden Mehrspur-Geräte zum Massenware. Ergo: Die Freunde gingen - aber die Schulden blieben... Doch wie werden aus analogen Daten digitale Daten, also Bits und Bytes? Man kann ja analoge Audiodaten als einen Graph darstellen (mehr dazu im Kapitel über Akustik). Der Kurvenverlauf existiert dann auf dem Papier oder auf dem Display eines Oszillographen.
Diesen Kurvenverlauf kann man auch durch Zahlen darstellen. Damit sind wir beim eigentlichen Thema:
Eine Sounddatei besteht aus vielen Bytes. Der Zahlenwert eines jeden Bytes drückt aus, auf welcher Position der Y-Achse sich der Graph gerade befindet. Bei positiven Werten befindet sich die Kurve oberhalb der Mittellinie, bei negativen Werten unterhalb davon.
Die Bitrate sagt aus, mit welcher Genauigkeit der Punkt einer Kurve bestimmt werden soll. Wenn die Genauigkeit 16 bit beträgt, kann der Wert des Samples zwischen -32767 und 32767 liegen, und die eigentliche Position der analogen Kurve wird auf den nächstliegenden Wert gerundet.
Die Samplefrequenz sagt aus, wieviele Samples in einer Sekunde verwendet werden sollen, um den Verlauf der Schwingungskurve festzuhalten. Eine Samplefrequenz von 44.1 kHz bedeutet, daß 44100 mal pro Sekunde der Abstand der Kurve vom Nullpunkt festgehalten wird (sprich: 44100 Samples pro Sekunde werden aufgezeichnet).
Man kann anhand der Auflösung auch den Speicherverbrauch einer WAV-Datei berechnen: bei 16-bit-Auflösung werden pro Sample 2 Byte verbraucht (8 bit = 1 Byte / 16 bit = 2 Byte pro Sample). Wenn 44.100 mal pro Sekunde abgetastet wird, werden 2 x 44.100 Bytes pro Sekunde verbraucht. Bei Stereo verdoppelt sich der benötigte Speicherplatz, weil ja der linke und rechte Kanal getrennt aufgezeichnet werden.
1 Sekunde in CD-Qualität = 2 x 44.100 x 2 bytes = 176.400 Bytes, also ca. 172 KB.
1 Minute in CD-Qualitat = 2 x 44.100 x 2 x 60 bytes = 10.584.000 Bytes, also ca. 10 MB.
Diese Werte haben nun, wie man aus eigener Erfahrung weiß, bedeutenden Einfluß auf die Qualität der Audiodaten. Je höher die Samplefrequenz ist, desto höhere Frequenzen können wiedergegeben werden. Eine Samplefrequenz von 44.100 Hz kann alle Frequenzen bis 22.0050 Hz wiedergeben, da eine Schwingung aus einer Auf- und Abbewegung besteht und von daher 2 Samples benötigt. Wenn die Samplefrequenz auf 11025 Hz verkleinert wird, werden alle Frequenzen über 5512.5 Hz abgeschnitten, so daß die Sounddatei dumpf klingt, so als ob man den Treble-Regler eines Equalizers herunterdreht.
Das menschliche Gehör kann alle Frequenzen von etwa 20 bis 16.000 Hz wahrnehmen, wobei mit zunehmendem Alter die höheren Frequenzen schlechter wahrgenommen werden. Die Samplerate sollte also (wenn möglich) mindestens 32 kHz betragen, besser 44.1 kHz, dies ist nämlich die Samplerate einer gewöhnlichen Audio-CD. Eine höhere Samplerate ist (jedenfalls zum Abhören) nicht sinnvoll, da sie hier keine Verbesserungen bringt. Außerdem können die meisten Mikrophone nur Frequenzen bis 20.000 hz aufnehmen.
Im Zusammenhang mit der Veränderung der Frequenz bei digitalen Audiodaten taucht oft das Wort Interpolation auf. Wenn man eine Sounddatei mit 11.025 Hz in eine 44.1 kHz Datei umrechnen will, muß man zwischen jedes Sample drei weitere Samples setzen. Ohne Interpolation hätten die drei folgenden Samples den gleichen Wert wie das erste Sample, und es würden Abstufungen entstehen, welche dann als sog. Obertöne erscheinen und hörbare Verzerrungen hervorrufen.[/B]
Lineare Interpolation besteht nun darin, eine Linie zwischen den Kanten der Abstufung zu ziehen und die drei Samples daran quasi "aufzureihen". Dies vermeidet Störgeräusche, entspricht aber noch nicht dem Charakter, in dem Wellenformen wiedergegeben werden. Gute Software berechnet zwischen den einelnen Samples eine Kurve, an der sich die hinzugefügten Samples orientieren.
Durch diese Methode werden Obertöne verhindert. Die Interpolationsroutinen sind sehr wichtig bei Sampling, da dort oft ein Sample von einer niedrigen auf eine höhere Samplerate umgerechnet werden muß und umgekehrt. Allerdings werden diese Obertöne gelegentlich als gewolltes Stilmittel eingesetzt. Sie erzeugen nämlich zusätzliche Töne, die den Klang höhenreicher und prägnanter klingen lassen, ihn quasi "aufrauhen".
Was 16 und 24 bit Auflösung wirklich bringt
Die Bitrate bestimmt, ob auch leisere Anteile einer Klanginformation wiedergegeben werden. Wenn die Bitrate z.B. 8 bit beträgt, kann die kleinste hörbare Schwingung gerade einmal 1/265stel des gesamten Abschnittes auf der Y-Achse betragen. Alle Klanganteile, die eine Amplitude von weniger als 1/256stel haben, wissenschaftlich ausgedrückt, alle Klanginformationen, die leiser als -45 dezibel (db) sind, werden nicht wiedergegeben. Der Graph einer Klanginformation kann nun nicht mehr präzise nachgebildet werden, so daß Verzerrungen entstehen, die als Rauschen hörbar sind.
Man spricht daher von einer "signal-to-noise ratio" von 0 zu -45 db, d.h., bei 8 bit Auflösung kann durch Verzerrungen ein Rauschen von bis zu -45db entstehen. Mehr über die Einheit "dezibel" steht im Kapitel über Akustik. Bei 16 bit Auflösung ist die "signal-to-noise ratio" bereits -96db, was in der Praxis als sauberer Klang hörbar ist, denn schon Klänge mit einer Amplitude von 1/65536stel werden wiedergegeben.
Nun gibt es immer mehr Soundkarten, die mit 24 bit Auflösung arbeiten. Diese hohe Auflösung ist bei 2 Problemen hilfreich: Bei Klangpassagen, die sehr leise sind (-60 bis -80 db), wie sie manchmal bei klassischer Musik auftreten, hört man ein leichtes Rauschen. Nun ja, jede Mittelklasse-HiFi-Anlage hat ein höheres Grundrauschen als das sog. Quantisierungs-Rauschen. Wer Flöhe husten hört oder fest an 24 bit glaubt, wird möglicherweise Unterschiede hören. Otto Normal und auch viele Tonstudios arbeiten immer noch erfolgreich mit 16 bit Auflösung.
Die höhere Bitrate beseitigt dafür aber einen schon eher hörbaren Nachteil von 16 bit Dateien: Je öfter sie bearbeitet werden, desto mehr Informationen gehen verloren. Es ergeben sich Rundungsfehler, die bei jeder neuen Bearbeitung zunehmen. Aber auch hier muß man schon extrem oft das Audiofile durch diverse Bearbeitungsstufen durchnudeln, um Quantisierungsrauschen zu hören.
Wegen der immer größer werdenden Speicherkapazität von Computern ist es aber nur noch eine Frage der Zeit, bis 24 bit Auflösung die Standard-Bitrate für Soundkarten und Sound-Editoren ist. Wavelab unterstützt 20 und 24 bit Auflösung, Cooledit Pro sogar 32 bit.
Um Klanginformationen hörbar zu machen, die zu leise sind, um mit der jeweiligen Bitrate wiedergegeben werden zu können, bedient man sich einer speziellen Technik: "Dither" und "Noise Shaping".
Zur Erklärung, wie "Dithering" funktioniert, ist es notwendig, sich noch einmal den oben beschriebenen Graphen als Zahlenmodell vor Augen zu führen. In unserem Beispiel soll der Wert der Y-Achse in einer Sekunde vom Wert 12345 zu 12346 wandern. Da er aber sich nur auf einem der beiden Y-Positionen befinden kann und nicht dazwischen, müßte er konsequenterweise eine halbe Sekunde auf Wert 12345 bleiben und dann zu dem Wert 12346 springen, wo er auch eine halbe Sekunde bleibt.
Man spricht von "Rundungsfehlern", daß digitale Werte nur ganze Zahlen annehmen können. Um aber trotzdem eine analoge Kurve präzise digital abbilden zu können, wird ein kleiner Trick angewendet: Die Position der der Y-Achse "hüpft" immer zwischen dem Wert 12345 und 12346 hin- und her. Je nachdem, wie oft er sich an einem der beiden Werte befindet, wird die Linie nachgezeichnet. Am Anfang springt der Bleistift nur selten zu Punkt 12346, nach einer halben Sekunde befindet er sich abwechselnd zwischen den Werten 12345 und 12346 und am Ende ist er fast nur noch auf Position 12346.
Dieses "Hüpfen" wird "dither" genannt. Es hat den Nachteil, daß es als sehr leises Rauschen hörbar ist. Durch "Noise Shaping" wird das Rauschen in sehr hohe Frequenzen verlagert, so daß es vom menschlichen Ohr nicht mehr wahrgenommen wird. "Noise Shaping" sollte aber nur bei 44.1 kHz Sounddateien angewendet werden. Bei 22.05 kHz Samplefrequenz kann "Noise Shaping" das Rauschen nur bis 11.025 hz verlagern, so daß es deutlich hörbar ist. Grund dafür ist die mathematische Tatsache, daß der hörbare Frequenzbereich immer nur halb so groß wie die Abtastrate (=Samplefrequenz) ist. Man sollte deshalb im Normalfall "Dithering" nur bei einer Abtastrate von 44.100 hz einsetzen.
Diesen Kurvenverlauf kann man auch durch Zahlen darstellen. Damit sind wir beim eigentlichen Thema:
Eine Sounddatei besteht aus vielen Bytes. Der Zahlenwert eines jeden Bytes drückt aus, auf welcher Position der Y-Achse sich der Graph gerade befindet. Bei positiven Werten befindet sich die Kurve oberhalb der Mittellinie, bei negativen Werten unterhalb davon.
Die Bitrate sagt aus, mit welcher Genauigkeit der Punkt einer Kurve bestimmt werden soll. Wenn die Genauigkeit 16 bit beträgt, kann der Wert des Samples zwischen -32767 und 32767 liegen, und die eigentliche Position der analogen Kurve wird auf den nächstliegenden Wert gerundet.
Die Samplefrequenz sagt aus, wieviele Samples in einer Sekunde verwendet werden sollen, um den Verlauf der Schwingungskurve festzuhalten. Eine Samplefrequenz von 44.1 kHz bedeutet, daß 44100 mal pro Sekunde der Abstand der Kurve vom Nullpunkt festgehalten wird (sprich: 44100 Samples pro Sekunde werden aufgezeichnet).
Man kann anhand der Auflösung auch den Speicherverbrauch einer WAV-Datei berechnen: bei 16-bit-Auflösung werden pro Sample 2 Byte verbraucht (8 bit = 1 Byte / 16 bit = 2 Byte pro Sample). Wenn 44.100 mal pro Sekunde abgetastet wird, werden 2 x 44.100 Bytes pro Sekunde verbraucht. Bei Stereo verdoppelt sich der benötigte Speicherplatz, weil ja der linke und rechte Kanal getrennt aufgezeichnet werden.
1 Sekunde in CD-Qualität = 2 x 44.100 x 2 bytes = 176.400 Bytes, also ca. 172 KB.
1 Minute in CD-Qualitat = 2 x 44.100 x 2 x 60 bytes = 10.584.000 Bytes, also ca. 10 MB.
Diese Werte haben nun, wie man aus eigener Erfahrung weiß, bedeutenden Einfluß auf die Qualität der Audiodaten. Je höher die Samplefrequenz ist, desto höhere Frequenzen können wiedergegeben werden. Eine Samplefrequenz von 44.100 Hz kann alle Frequenzen bis 22.0050 Hz wiedergeben, da eine Schwingung aus einer Auf- und Abbewegung besteht und von daher 2 Samples benötigt. Wenn die Samplefrequenz auf 11025 Hz verkleinert wird, werden alle Frequenzen über 5512.5 Hz abgeschnitten, so daß die Sounddatei dumpf klingt, so als ob man den Treble-Regler eines Equalizers herunterdreht.
Das menschliche Gehör kann alle Frequenzen von etwa 20 bis 16.000 Hz wahrnehmen, wobei mit zunehmendem Alter die höheren Frequenzen schlechter wahrgenommen werden. Die Samplerate sollte also (wenn möglich) mindestens 32 kHz betragen, besser 44.1 kHz, dies ist nämlich die Samplerate einer gewöhnlichen Audio-CD. Eine höhere Samplerate ist (jedenfalls zum Abhören) nicht sinnvoll, da sie hier keine Verbesserungen bringt. Außerdem können die meisten Mikrophone nur Frequenzen bis 20.000 hz aufnehmen.
Im Zusammenhang mit der Veränderung der Frequenz bei digitalen Audiodaten taucht oft das Wort Interpolation auf. Wenn man eine Sounddatei mit 11.025 Hz in eine 44.1 kHz Datei umrechnen will, muß man zwischen jedes Sample drei weitere Samples setzen. Ohne Interpolation hätten die drei folgenden Samples den gleichen Wert wie das erste Sample, und es würden Abstufungen entstehen, welche dann als sog. Obertöne erscheinen und hörbare Verzerrungen hervorrufen.[/B]
Lineare Interpolation besteht nun darin, eine Linie zwischen den Kanten der Abstufung zu ziehen und die drei Samples daran quasi "aufzureihen". Dies vermeidet Störgeräusche, entspricht aber noch nicht dem Charakter, in dem Wellenformen wiedergegeben werden. Gute Software berechnet zwischen den einelnen Samples eine Kurve, an der sich die hinzugefügten Samples orientieren.
Durch diese Methode werden Obertöne verhindert. Die Interpolationsroutinen sind sehr wichtig bei Sampling, da dort oft ein Sample von einer niedrigen auf eine höhere Samplerate umgerechnet werden muß und umgekehrt. Allerdings werden diese Obertöne gelegentlich als gewolltes Stilmittel eingesetzt. Sie erzeugen nämlich zusätzliche Töne, die den Klang höhenreicher und prägnanter klingen lassen, ihn quasi "aufrauhen".
Was 16 und 24 bit Auflösung wirklich bringt
Die Bitrate bestimmt, ob auch leisere Anteile einer Klanginformation wiedergegeben werden. Wenn die Bitrate z.B. 8 bit beträgt, kann die kleinste hörbare Schwingung gerade einmal 1/265stel des gesamten Abschnittes auf der Y-Achse betragen. Alle Klanganteile, die eine Amplitude von weniger als 1/256stel haben, wissenschaftlich ausgedrückt, alle Klanginformationen, die leiser als -45 dezibel (db) sind, werden nicht wiedergegeben. Der Graph einer Klanginformation kann nun nicht mehr präzise nachgebildet werden, so daß Verzerrungen entstehen, die als Rauschen hörbar sind.
Man spricht daher von einer "signal-to-noise ratio" von 0 zu -45 db, d.h., bei 8 bit Auflösung kann durch Verzerrungen ein Rauschen von bis zu -45db entstehen. Mehr über die Einheit "dezibel" steht im Kapitel über Akustik. Bei 16 bit Auflösung ist die "signal-to-noise ratio" bereits -96db, was in der Praxis als sauberer Klang hörbar ist, denn schon Klänge mit einer Amplitude von 1/65536stel werden wiedergegeben.
Nun gibt es immer mehr Soundkarten, die mit 24 bit Auflösung arbeiten. Diese hohe Auflösung ist bei 2 Problemen hilfreich: Bei Klangpassagen, die sehr leise sind (-60 bis -80 db), wie sie manchmal bei klassischer Musik auftreten, hört man ein leichtes Rauschen. Nun ja, jede Mittelklasse-HiFi-Anlage hat ein höheres Grundrauschen als das sog. Quantisierungs-Rauschen. Wer Flöhe husten hört oder fest an 24 bit glaubt, wird möglicherweise Unterschiede hören. Otto Normal und auch viele Tonstudios arbeiten immer noch erfolgreich mit 16 bit Auflösung.
Die höhere Bitrate beseitigt dafür aber einen schon eher hörbaren Nachteil von 16 bit Dateien: Je öfter sie bearbeitet werden, desto mehr Informationen gehen verloren. Es ergeben sich Rundungsfehler, die bei jeder neuen Bearbeitung zunehmen. Aber auch hier muß man schon extrem oft das Audiofile durch diverse Bearbeitungsstufen durchnudeln, um Quantisierungsrauschen zu hören.
Wegen der immer größer werdenden Speicherkapazität von Computern ist es aber nur noch eine Frage der Zeit, bis 24 bit Auflösung die Standard-Bitrate für Soundkarten und Sound-Editoren ist. Wavelab unterstützt 20 und 24 bit Auflösung, Cooledit Pro sogar 32 bit.
Um Klanginformationen hörbar zu machen, die zu leise sind, um mit der jeweiligen Bitrate wiedergegeben werden zu können, bedient man sich einer speziellen Technik: "Dither" und "Noise Shaping".
Zur Erklärung, wie "Dithering" funktioniert, ist es notwendig, sich noch einmal den oben beschriebenen Graphen als Zahlenmodell vor Augen zu führen. In unserem Beispiel soll der Wert der Y-Achse in einer Sekunde vom Wert 12345 zu 12346 wandern. Da er aber sich nur auf einem der beiden Y-Positionen befinden kann und nicht dazwischen, müßte er konsequenterweise eine halbe Sekunde auf Wert 12345 bleiben und dann zu dem Wert 12346 springen, wo er auch eine halbe Sekunde bleibt.
Man spricht von "Rundungsfehlern", daß digitale Werte nur ganze Zahlen annehmen können. Um aber trotzdem eine analoge Kurve präzise digital abbilden zu können, wird ein kleiner Trick angewendet: Die Position der der Y-Achse "hüpft" immer zwischen dem Wert 12345 und 12346 hin- und her. Je nachdem, wie oft er sich an einem der beiden Werte befindet, wird die Linie nachgezeichnet. Am Anfang springt der Bleistift nur selten zu Punkt 12346, nach einer halben Sekunde befindet er sich abwechselnd zwischen den Werten 12345 und 12346 und am Ende ist er fast nur noch auf Position 12346.
Dieses "Hüpfen" wird "dither" genannt. Es hat den Nachteil, daß es als sehr leises Rauschen hörbar ist. Durch "Noise Shaping" wird das Rauschen in sehr hohe Frequenzen verlagert, so daß es vom menschlichen Ohr nicht mehr wahrgenommen wird. "Noise Shaping" sollte aber nur bei 44.1 kHz Sounddateien angewendet werden. Bei 22.05 kHz Samplefrequenz kann "Noise Shaping" das Rauschen nur bis 11.025 hz verlagern, so daß es deutlich hörbar ist. Grund dafür ist die mathematische Tatsache, daß der hörbare Frequenzbereich immer nur halb so groß wie die Abtastrate (=Samplefrequenz) ist. Man sollte deshalb im Normalfall "Dithering" nur bei einer Abtastrate von 44.100 hz einsetzen.